After an extended hiatus, Reproducible Finance is back! We’ll celebrate by changing focus a bit and coding up an investment strategy called Momentum. Before we even tiptoe in that direction, please note that this is not intended as investment advice and it’s not intended to be a script that can be implemented for trading. The goal is to explore some R code flows applied to a real-world project. Don’t live-trade this at home!
Back to the substance of the day, the theory behind momentum investing is that an asset that has done well in the recent past will continue to do so. It’s not “buy low and sell high”. It’s “buy high, and sell higher”! What might explain this anomaly? Behavioral economics has some possible answers, like anchoring, disposition, and herding.
In practice, momentum entails a look back into the past to determine whether an asset has exceeded some benchmark, and if it has, buy and hold that asset for some time into the future. That’s completely flying in the face of the efficient market hypothesis because it’s positing that the past is somehow giving us information that has not been reflected in the current price of the asset.
There’s a plethora of fascinating research on momentum investing; here’s a sampling.
The seminal academic paper is Returns to Buying Winners and Selling Losers: Implications for Stock Market Efficiency by Jegadeesh and Titman from way back in 1993.
An excellent primer on the philosophy of momentum (and where I would recommend to start) is this piece from Alpha Architect. From there, AA also has a treasure trove of momentum posts here. More recently, there are two excellent and more advanced research papers from ReSolve Asset Management, with some excellent data visualizations, and Newfound Research, with a concise explanation of the strategy logic.
That’s a lot of material - here’s a short quotation from Fama and French by way of Alpha Architect that should provide us plenty of motivation:
“The premier anomaly is momentum.” 1
Let’s get to it and load up some packages.
library(tidyverse)
library(highcharter)
library(tibbletime)
library(tidyquant)
library(timetk)
library(riingo)We are going to implement a simplified version of a momentum strategy that deals with 4 assets:
+ SPY, an SP500 ETF
+ EFA, a global equities ETF
+ AGG, a bond ETF
+ TLT, a treasuries ETFThe strategy logic goes as follows: compare the previous twelve months’ returns of the SP500 (SPY) to treasury bonds (TLT). If the returns of SPY do not exceed those of TLT, hold bonds (AGG) for the next month. If SPY returns do exceed TLT, compare the previous 12 months’ returns of the SP500 to the non-US equities (EFA). Whichever of SP500 or non-US equities had the higher previous twelve months’ returns, hold that asset for the next month. Thus, each month, our strategy will hold either AGG, SPY or EFA and we reexamine at the end of each month. That’s twelve look-backs per year, and twelve possible buy/sell transactions per year.
Here is the trading logic broken down into more code-oriented steps: 1) Import prices for SPY, TLT, AGG and EFA 2) Convert to monthly prices 3) Convert AGG to monthly returns 4) Convert TLT to twelve months’ returns 5) Convert SPY and EFA to both monthly and twelve month’s returns 6) Each month, compare previous twelve months’ SPY returns to those of TLT; if TLT exceeds SPY, hold AGG next month 7) Else, compare previous twelve months’ SPY returns to EFA 8) If previous twelve months’ SPY returns exceeded those of EFA, hold SPY next month 9) If previous twelve months’ EFA returns exceeded those of SPY, hold EFA next month
Let’s start by importing the price data from tiingo. We used tiingo via the riingo package in a previous post, if you’d like to see it in a different context and get a bit more explanation.
We’ll first create a vector that holds tickers for SPY, AGG, EFA and TLT, and then pass that vector to riingo_prices().
# riingo requires an API key. You can get one free from tiingo.com
# riingo_set_token("your API key here")
symbols <-
c("SPY", "AGG", "EFA", "TLT")
symbols %>%
riingo_prices(.,
start_date = "2000-01-01",
end_date = "2018-12-31") %>%
mutate(date = ymd(date)) %>%
# see what happens if don't group_by here
group_by(ticker) %>%
slice(1)# A tibble: 4 x 14
# Groups: ticker [4]
ticker date close high low open volume adjClose adjHigh adjLow
<chr> <date> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl>
1 AGG 2003-09-26 102. 102. 102 102 1.18e4 60.9 60.9 60.7
2 EFA 2001-08-17 126. 126. 125. 126 1.61e5 27.0 27.0 26.9
3 SPY 2000-01-03 145. 148. 144. 148. 8.16e6 101. 103. 100.
4 TLT 2002-07-26 82.5 82.8 82.4 82.7 3.16e5 44.6 44.7 44.5
# … with 4 more variables: adjOpen <dbl>, adjVolume <int>, divCash <dbl>,
# splitFactor <dbl>We imported price data for each of our ETFs, but they don’t have the same inception dates. AGG launched in September of 2003, so that’s when we’ll be constrained to as a start date. We will have about 15 years of data.
As noted above, our strategy is tied to a monthly periodicity, looking back twelve months to determine if we wish to hold a certain asset for the next month. Let’s convert our daily prices to monthly prices with tq_transmute(select = adjClose, mutate_fun = to.monthly, indexAt = "lastof") from the tidyquant package. We are telling that function to convert the column called ‘adjClose’ to monthly prices, and anchored to the end of the month. We will store the results in an object called prices_monthly.
prices_monthly <-
symbols %>%
riingo_prices(.,
start_date = "2000-01-01",
end_date = "2018-12-31") %>%
mutate(date = ymd(date)) %>%
group_by(ticker) %>%
tq_transmute(select = adjClose, mutate_fun = to.monthly, indexAt = "lastof")Let’s use slice(1, n()) to grab the first and last observation for each of our funds. The last observation is considered the nth observation here.
prices_monthly %>%
slice(1, n())# A tibble: 8 x 3
# Groups: ticker [4]
ticker date adjClose
<chr> <date> <dbl>
1 AGG 2003-09-30 61.1
2 AGG 2018-12-31 105.
3 EFA 2001-08-31 26.8
4 EFA 2018-12-31 58.8
5 SPY 2000-01-31 97.3
6 SPY 2018-12-31 249.
7 TLT 2002-07-31 44.6
8 TLT 2018-12-31 120. We have monthly prices for our funds, with differing start dates and a common end date. Now let’s start to wrangle this data into a format that is suited for our strategy’s logic. Recall that we wish to implement this flow:
- If prev twelve months’ SPY returns is lower than TLT’s, buy/hold AGG this month, else move to step 2.
- If prev twelve months’ SPY is higher then prev twelve months’ EFA, buy/hold SPY this month, else move to step 3.
- If prev twelve months’ EFA is higher then prev twelve months’ SPY, buy/hold EFA this month.
Since we need to compare the past twelve months’ return of SPY to that of TLT and then to that of EFA, it will be nice if those twelve months’ returns for each asset are in three separate columns. That means we’ll want a tibble with one column for twelve month’s returns of SPY, one column for twelve months’ returns of TLT, and one column for 12 months’ returns of EFA.
Honestly, that last sentence makes me pause and wonder if I’m doing something totally wrong. Any time I start taking data that is tidy and making it wider, I stop and think about why I need to do that. There is currently one column for prices, one column for the date, and one column for the ticker name.
# A tibble: 8 x 3
# Groups: ticker [4]
ticker date adjClose
<chr> <date> <dbl>
1 AGG 2003-09-30 61.1
2 AGG 2003-10-31 60.5
3 EFA 2001-08-31 26.8
4 EFA 2001-09-30 24.2
5 SPY 2000-01-31 97.3
6 SPY 2000-02-29 95.8
7 TLT 2002-07-31 44.6
8 TLT 2002-08-31 47.0To me, by putting those symbols in one column, we are treating them as being the same variable but different categories or groups of that variable. However, our trading logic treats them as different classes of assets entirely, not just different groups within the same thing called ‘ticker’. Plus, it’s easier to compare these assets with if_else() logic when they are in different columns. So, we’ll take this nice, tidy tibble of ETF prices and make it wider with different returns data.
Let’s get to it and hopefully that will make sense.
Since we are going to be calculating monthly and rolling twelve month returns for several assets and mashing them together, let’s run the calculations in pieces then join them. We’ll start with TLT, which means using filter(ticker == "TLT"). Then we’ll use mutate() to calculate twelve-month returns. Notice that we use quite verbose names for the new column, e.g., tbill_twelve_mon_ret. That will get cumbersome, but it will also help our human eyes to quickly glance at our end data and find the new columns.
n_lag <- 12
risk_free_tlt <-
prices_monthly %>%
filter(ticker == "TLT") %>%
mutate(tbill_twelve_mon_ret = ((adjClose / lag(adjClose, n_lag)) - 1)) %>%
# Why ungroup here? If we don't tibble won't let us delete the ticker column
ungroup() %>%
select(-adjClose, -ticker) %>%
na.omit()
risk_free_tlt %>%
head()# A tibble: 6 x 2
date tbill_twelve_mon_ret
<date> <dbl>
1 2003-07-31 0.0535
2 2003-08-31 0.0115
3 2003-09-30 0.0279
4 2003-10-31 0.0350
5 2003-11-30 0.0481
6 2003-12-31 0.0162We calculated just the twelve months’ returns and did not include the one month return, because our logic does not contemplate holding this asset for even a month. We use AGG for our bond exposure. But, the twelve months’ returns of AGG are not part of our logic, so we won’t calculate that. This is another reason to break up these returns calculations and then do a big join at the end.
We will calculate the one month returns of AGG with the exact same code, except we lag by one instead of twelve.
bond_returns <-
prices_monthly %>%
filter(ticker == "AGG") %>%
mutate(bond_return = ((adjClose / lag(adjClose, 1)) - 1)) %>%
ungroup() %>%
select(-adjClose, -ticker) %>%
na.omit()
bond_returns %>%
head()# A tibble: 6 x 2
date bond_return
<date> <dbl>
1 2003-10-31 -0.00935
2 2003-11-30 0.00335
3 2003-12-31 0.00979
4 2004-01-31 0.00441
5 2004-02-29 0.0114
6 2004-03-31 0.00684For EFA and SPY, we need to calculate both twelve months’ returns and one month returns. The code flow for calculating their returns are identical. I’m not going to delete the ticker column from SPY, but I will rename it to mom_asset (just in case we want to try different assets later, or even use Shiny to dynamically choose different assets).
equities_ex_us_returns <-
prices_monthly %>%
filter(ticker == "EFA") %>%
mutate(ex_us_return = ((adjClose / lag(adjClose)) - 1),
ex_us_twelve_mon_ret = ((adjClose / lag(adjClose, n_lag)) -1)) %>%
ungroup() %>%
select(-adjClose, -ticker) %>%
na.omit()
sp_500_returns <-
prices_monthly %>%
filter(ticker == "SPY") %>%
mutate(spy_return = ((adjClose / lag(adjClose)) - 1),
spy_twelve_mon_ret = ((adjClose / lag(adjClose, n_lag)) - 1)) %>%
select(-adjClose) %>%
rename(mom_asset = ticker)We now have four tibbles of returns, and want to combine them to one tibble. They all have a column called date, so we can run a bunch of calls to left_join(..., by = "date").
joined_returns_tbl <-
sp_500_returns %>%
left_join(risk_free_tlt, by = "date") %>%
left_join(equities_ex_us_returns, by = "date") %>%
left_join(bond_returns, by = "date") %>%
na.omit()
joined_returns_tbl %>%
head()# A tibble: 6 x 8
# Groups: mom_asset [1]
mom_asset date spy_return spy_twelve_mon_… tbill_twelve_mo…
<chr> <date> <dbl> <dbl> <dbl>
1 SPY 2003-10-31 0.0535 0.209 0.0350
2 SPY 2003-11-30 0.0109 0.151 0.0481
3 SPY 2003-12-31 0.0503 0.282 0.0162
4 SPY 2004-01-31 0.0198 0.340 0.0411
5 SPY 2004-02-29 0.0136 0.377 0.0329
6 SPY 2004-03-31 -0.0132 0.356 0.0619
# … with 3 more variables: ex_us_return <dbl>, ex_us_twelve_mon_ret <dbl>,
# bond_return <dbl>Alright, we now have one massive tibble called joined_returns_tbl with eight columns. Those verbose names will come in handy here. For example, if we want to see all our twelve month calculations, we can use select(date, contains("twelve")) to grab each column whose name contains the string “twelve”.
joined_returns_tbl %>%
select(date, contains("twelve")) %>%
head()# A tibble: 6 x 5
# Groups: mom_asset [1]
mom_asset date spy_twelve_mon_r… tbill_twelve_mon… ex_us_twelve_mo…
<chr> <date> <dbl> <dbl> <dbl>
1 SPY 2003-10-31 0.209 0.0350 0.285
2 SPY 2003-11-30 0.151 0.0481 0.247
3 SPY 2003-12-31 0.282 0.0162 0.398
4 SPY 2004-01-31 0.340 0.0411 0.477
5 SPY 2004-02-29 0.377 0.0329 0.544
6 SPY 2004-03-31 0.356 0.0619 0.581We selected twelve months’ returns for SPY, EFA, and TLT so we can quickly glance at the new data and make sure it looks how we were expecting.
Next, we’ll implement the trading logic, which is, to repeat:
- If previous twelve months SP500 returns are lower than treasuries, buy/hold bonds via AGG this month, else to next step.
- If previous twelve months SP500 returns higher than EFA (equities ex us proxy), buy/hold SP500 this month.
- If previous twelve months EFA returns higher than SP500, buy/hold EFA this month.
We can implement this using the if_else() function from dplyr, and we’ll place those if_else() calls inside mutate(). To implement step one, we write
if_else(lag(spy_twelve_mon_ret) < lag(tbill_twelve_mon_ret), bond_return, which in English says if the lagged 12-month SPY return is less than the lagged 12-month TLT return, then this month we invest in AGG, or we book the one month return of AGG. We follow that with the else logic,
if_else(lag(spy_twelve_mon_ret) > lag(ex_us_twelve_mon_ret), spy_return, and that with our final else logic, ex_us_return. We labeled the new column that holds the results of those if_else() statements as strat_returns.
It might be interesting or important to know when the strategy is holding AGG, SPY, or EFA, so let’s create a column called strat_label that has the values bond, spy, and ex-us depending on where the strategy invests. That would allow us to calculate and visualize, for example, the proportion of time spent invested in EFA.
joined_returns_tbl %>%
# encode logic, if ticker higher than tbill, we could complicate this by adding in other
# assets for comparison.
mutate(strat_returns = if_else(lag(spy_twelve_mon_ret) < lag(tbill_twelve_mon_ret),
bond_return,
if_else(lag(spy_twelve_mon_ret) > lag(ex_us_twelve_mon_ret),
spy_return,
ex_us_return)),
strat_label = if_else(lag(spy_twelve_mon_ret) < lag(tbill_twelve_mon_ret),
"bond",
if_else(lag(spy_twelve_mon_ret) > lag(ex_us_twelve_mon_ret),
"spy",
"ex_us"))) %>%
na.omit() %>%
select(date, contains("strat")) %>%
head()# A tibble: 6 x 4
# Groups: mom_asset [1]
mom_asset date strat_returns strat_label
<chr> <date> <dbl> <chr>
1 SPY 2003-11-30 0.0253 ex_us
2 SPY 2003-12-31 0.0834 ex_us
3 SPY 2004-01-31 0.0113 ex_us
4 SPY 2004-02-29 0.0230 ex_us
5 SPY 2004-03-31 0.000707 ex_us
6 SPY 2004-04-30 -0.0339 ex_us All right, the logic or the signal is encoded. Let’s add a column for a 80/20 SPY/AGG portfolio as a sort of buy and hold benchmark and then save the whole massive tibble as strat_returns.
strat_returns <-
joined_returns_tbl %>%
# encode logic, if ticker higher than tbill, we could complicate this by adding in other
# assets for comparison.
mutate(strat_returns = if_else(lag(spy_twelve_mon_ret) < lag(tbill_twelve_mon_ret),
bond_return,
if_else(lag(spy_twelve_mon_ret) > lag(ex_us_twelve_mon_ret),
spy_return,
ex_us_return)),
strat_label = if_else(lag(spy_twelve_mon_ret) < lag(tbill_twelve_mon_ret),
"bond",
if_else(lag(spy_twelve_mon_ret) > lag(ex_us_twelve_mon_ret),
"spy",
"ex_us")),
bench_returns = (.8 * spy_return) + (.2 * bond_return)) %>%
na.omit() %>%
select(date, bench_returns, contains("strat"))Let’s see how frequently we are invested in bonds versus SPY versus equities ex-USA.
strat_returns %>%
count(strat_label) %>%
mutate(prop = prop.table(n))# A tibble: 3 x 4
# Groups: mom_asset [1]
mom_asset strat_label n prop
<chr> <chr> <int> <dbl>
1 SPY bond 63 0.346
2 SPY ex_us 65 0.357
3 SPY spy 54 0.297Let’s visualize the same data with a bar chart using geom_col() and the height set to the proportion of months in each asset. Instead of using a legend, or placing the labels on the x-axis, we will place them on the chart above the bars.
First we add the labels with geom_label(aes(label = strat_label) and let’s make them white with fill = "white". We can remove the legend with theme(legend.position = "none") and the x-axis text can be removed with theme(...axis.text.x = element_blank(), axis.ticks = element_blank()).
strat_returns %>%
count(strat_label) %>%
mutate(prop = prop.table(n)) %>%
ggplot(aes(x = strat_label, y = prop, fill = strat_label)) +
geom_col(width = .15) +
scale_y_continuous(labels = scales::percent) +
geom_label(aes(label = strat_label), vjust = -.5, fill = "white") +
ylab("relative frequencies") +
xlab("") +
expand_limits(y = .4) +
theme(legend.position = "none",
axis.text.x = element_blank(),
axis.ticks = element_blank()) 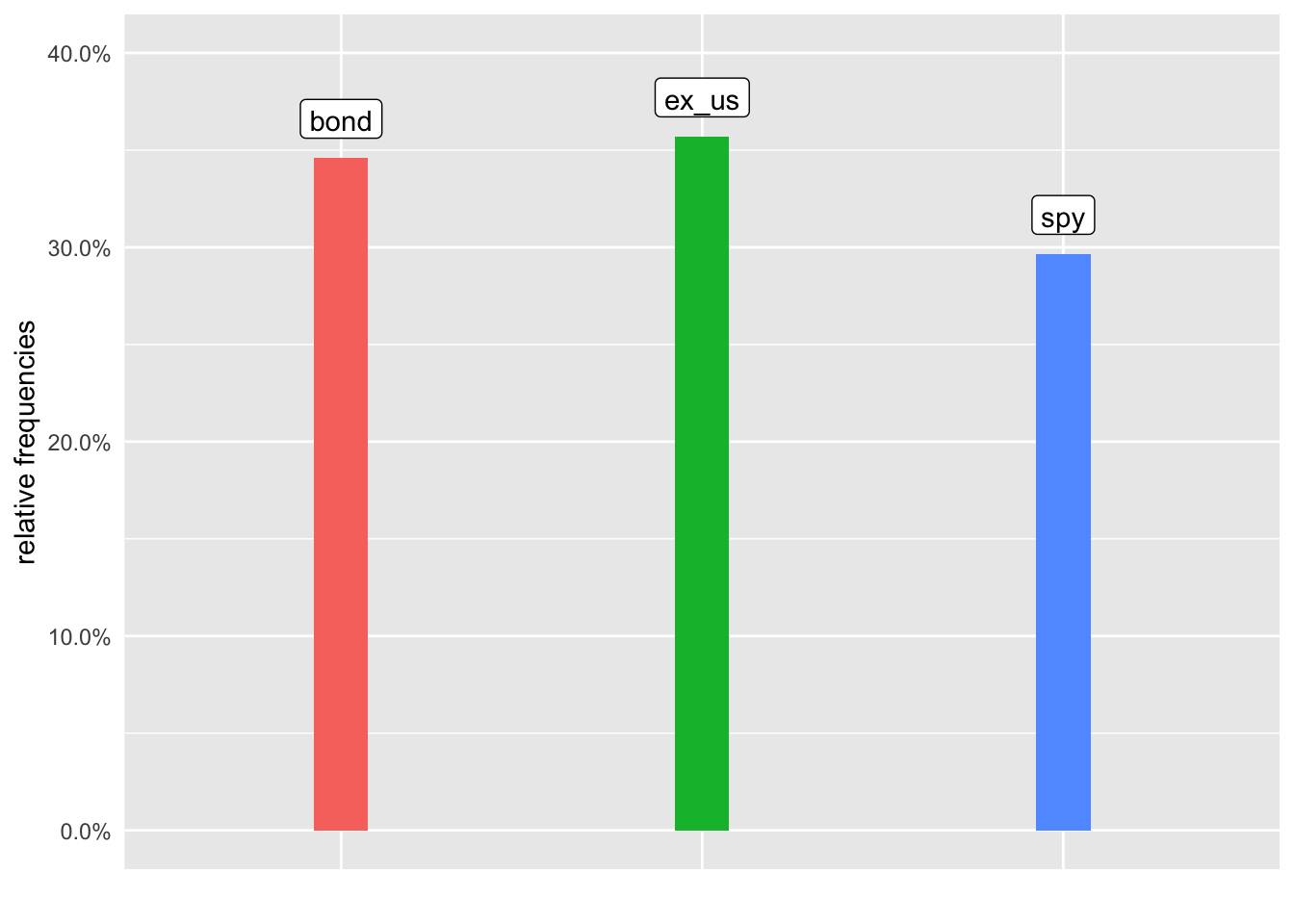
Since the data is in a nice, tidy format, we can also head straight to highcharter to build an interactive bar chart.
strat_returns %>%
count(strat_label) %>%
mutate(prop = prop.table(n)) %>%
hchart(., hcaes(x = strat_label, y = prop, color = strat_label),
type = "column",
pointWidth = 30) %>%
hc_tooltip(pointFormat = "{point.strat_label}: {point.prop: .2f}")Maybe we want to see the distribution of returns for each strategy. Here is a histogram of each using geom_histogram().
strat_returns %>%
ungroup() %>%
select(bench_returns, strat_returns) %>%
gather(type, returns) %>%
ggplot(aes(returns, color = type, fill = type)) +
geom_histogram(bins = 60) +
facet_wrap(~type)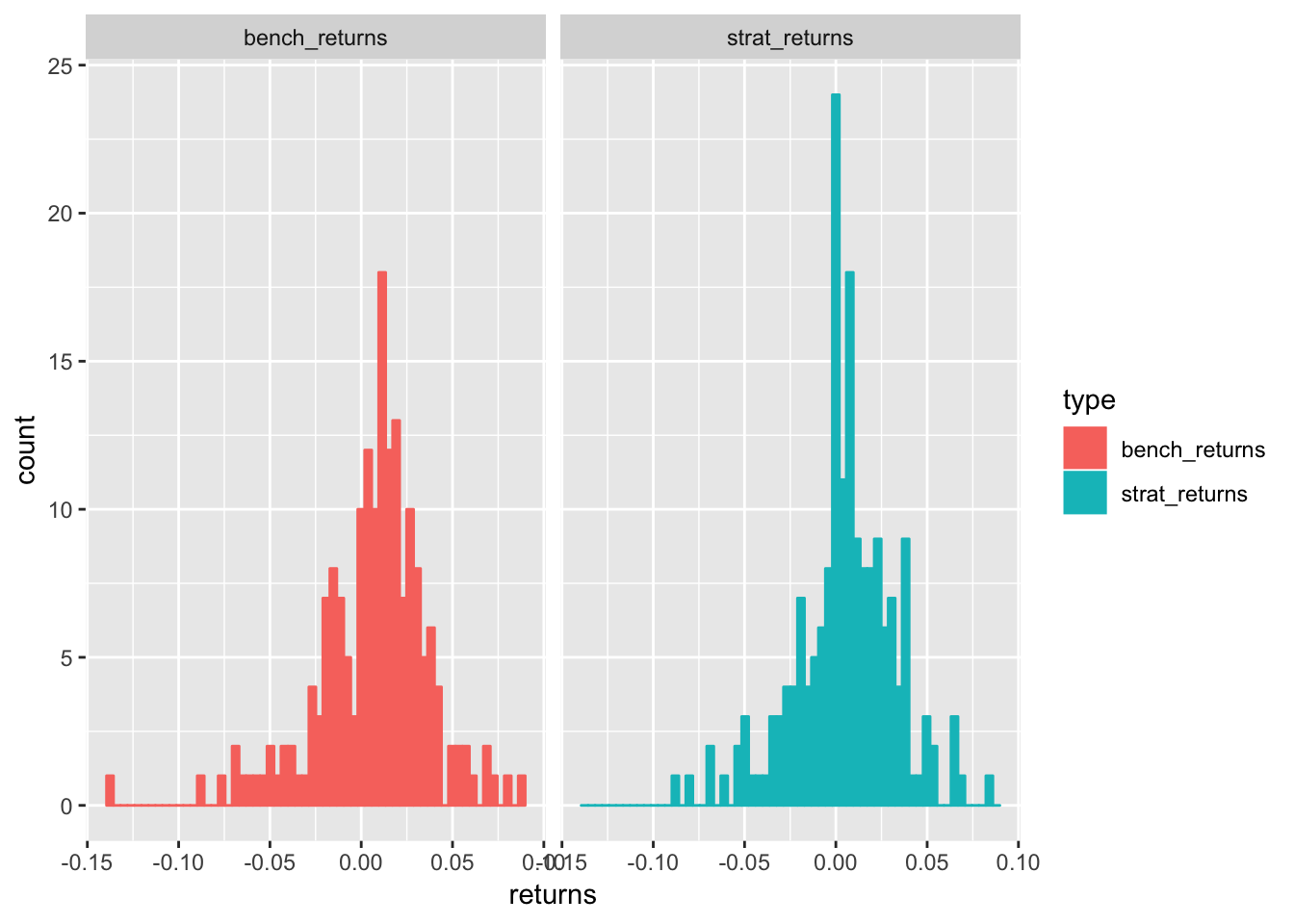
Here’s a horizontal box plot and violin chart built using a combination of gom_boxplot and geom_violin().
strat_returns %>%
ungroup() %>%
select(bench_returns, strat_returns) %>%
gather(type, returns) %>%
ggplot(aes(x = type, y = returns, color = type, fill = type)) +
geom_boxplot(width = 0.1, fill = "white")+
geom_violin(alpha = .05) +
coord_flip()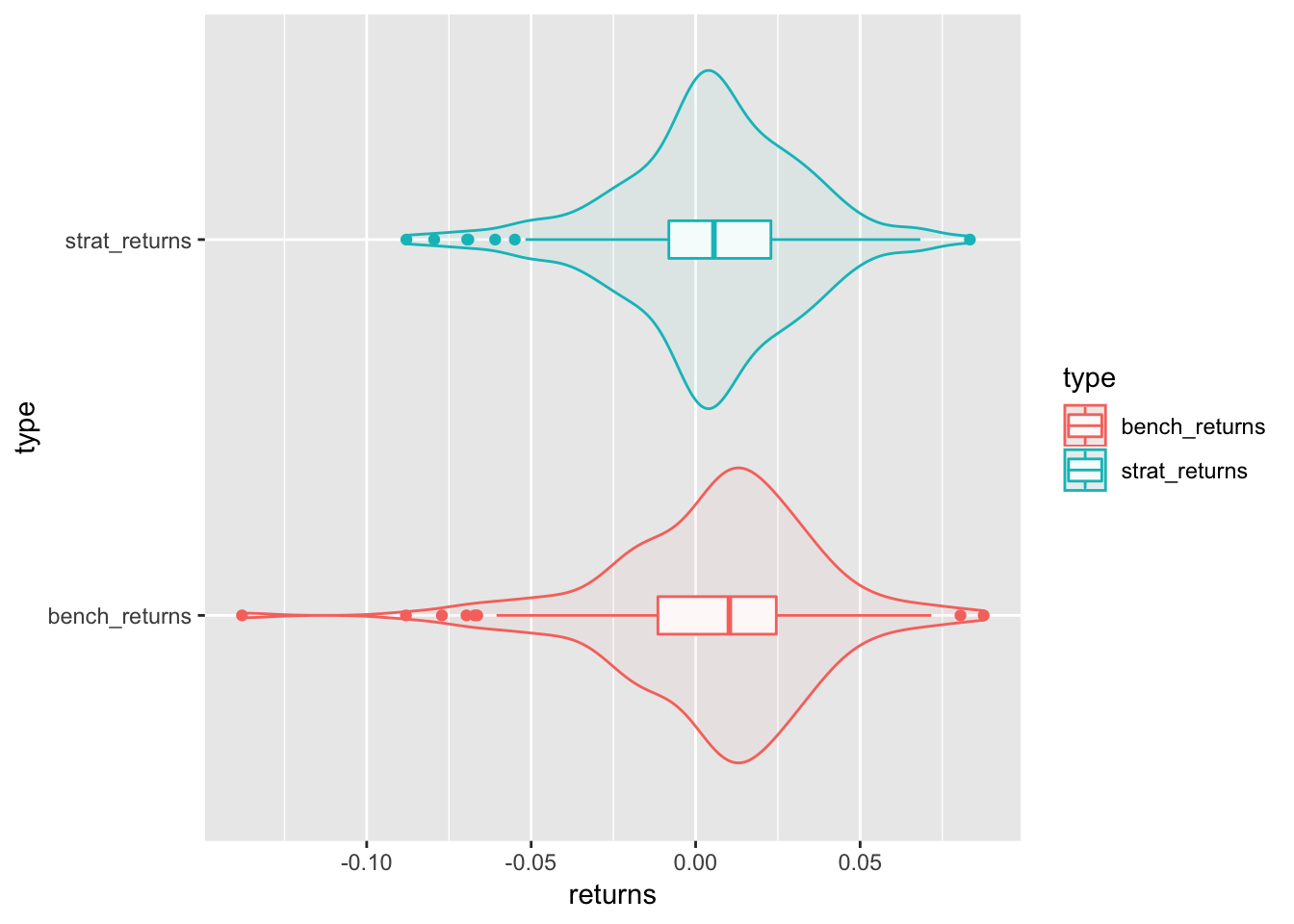
The distribution of returns is helpful, but let’s also have a look at which returns path delivered the highest growth. We won’t take account of risk here; we’ll just visualize how one dollar would have grown in each strategy. We will start with the seemingly underused accumulate() function from purrr to create two new columns called strat_growth and bench_growth. Then we use select(date, contains("growth")) to isolate just the date and growth columns.
strat_growth <-
strat_returns %>%
mutate(strat_growth = accumulate(1 + strat_returns, `*`),
bench_growth = accumulate(1 + bench_returns, `*`)) %>%
ungroup() %>%
select(date, contains("growth")) %>%
gather(strat, growth, -date)Now we can pipe strat_growth to hchart().
strat_growth %>%
hchart(., hcaes(x = date, y = growth, group = strat),
type = "line") %>%
hc_tooltip(pointFormat = "{point.strat}: ${point.growth: .2f}")Our momentum strategy did not grow as much as a pure buy-hold strategy. Let’s check some summary statistics by using tq_performance() and table.Stats.
strat_returns %>%
ungroup() %>%
select(date, strat_returns, bench_returns) %>%
gather(strats, returns, -date) %>%
group_by(strats) %>%
tq_performance(Ra = returns,
performance_fun = table.Stats) %>%
gather(stat, value, -strats)# A tibble: 32 x 3
# Groups: strats [2]
strats stat value
<chr> <chr> <dbl>
1 strat_returns ArithmeticMean 0.0046
2 bench_returns ArithmeticMean 0.0064
3 strat_returns GeometricMean 0.0042
4 bench_returns GeometricMean 0.0059
5 strat_returns Kurtosis 1.01
6 bench_returns Kurtosis 2.57
7 strat_returns LCLMean(0.95) 0.0005
8 bench_returns LCLMean(0.95) 0.0018
9 strat_returns Maximum 0.0834
10 bench_returns Maximum 0.0876
# … with 22 more rowsThus far, our strategy seems inferior to buy-hold. Let’s check the max drawdowns with the table.DownsideRisk function.
strat_returns %>%
ungroup() %>%
select(date, strat_returns, bench_returns) %>%
gather(strats, returns, -date) %>%
group_by(strats) %>%
tq_performance(Ra = returns,
performance_fun = table.DownsideRisk) %>%
gather(stat, value, -strats)# A tibble: 22 x 3
# Groups: strats [2]
strats stat value
<chr> <chr> <dbl>
1 strat_returns DownsideDeviation(0%) 0.0184
2 bench_returns DownsideDeviation(0%) 0.0213
3 strat_returns DownsideDeviation(MAR=10%) 0.0225
4 bench_returns DownsideDeviation(MAR=10%) 0.025
5 strat_returns DownsideDeviation(Rf=0%) 0.0184
6 bench_returns DownsideDeviation(Rf=0%) 0.0213
7 strat_returns GainDeviation 0.0176
8 bench_returns GainDeviation 0.0176
9 strat_returns HistoricalES(95%) -0.0622
10 bench_returns HistoricalES(95%) -0.0727
# … with 12 more rowsIf we isolate the MaximumDrawdown and VaR measures, we see this:
strat_returns %>%
ungroup() %>%
select(date, strat_returns, bench_returns) %>%
gather(strats, returns, -date) %>%
group_by(strats) %>%
tq_performance(Ra = returns,
performance_fun = table.DownsideRisk) %>%
select(MaximumDrawdown, contains("VaR"))# A tibble: 2 x 4
# Groups: strats [2]
strats MaximumDrawdown `HistoricalVaR(95%)` `ModifiedVaR(95%)`
<chr> <dbl> <dbl> <dbl>
1 strat_returns 0.172 -0.0482 -0.0435
2 bench_returns 0.422 -0.0496 -0.0503The momentum strat didn’t grow as much as buy-hold, but it had a far smaller max drawdown.
That’s all for today - thanks for reading!
A couple of plugs before we close:
If you like this sort of thing, check out my book, Reproducible Finance with R.
This is not specific to finance, but several of the stringr and ggplot tricks in this post came from this awesome Business Science University course.
Want to get into Momentum Investing? Have a look at this book Quantitative Momentum first.
Happy coding!
Fama, E. and K. French, 2008, Dissecting Anomalies, The Journal of Finance, 63, pg. 1653-1678.]↩
You may leave a comment below or discuss the post in the forum community.rstudio.com.